二分查找算法

1.什么是二分查找

二分查找算法也称折半查找，是一种非常高效的工作于有序数组的查找算法。

二分查找针对的是一个有序的数据集合，每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。

2.二分查找的基本实现

需求：在有序数组 nums 内，查找值 target

• 如果找到返回索引
• 如果找不到返回 -1

算法描述:

二分查找是在一个有序的数组中查找关键字target（一开始的下界low=0，上界high=nums.length - 1），需要将关键字与数组中间元素mid（mid=(low+high)/2向下取整）作比较：

1. target = mid，查找成功，返回mid下标

2. target > mid，目标在数组右半部分，low=mid+1

3. target < mid，目标在数组坐班部分，high=mid-1

二分查找运行时间为对数时间O(logn)，数组有n个元素，假设n是2的幂，第一次比较后剩下n/2个元素，第二次比较后剩下(n/2)/2个元素，以此类推，k次比较之后，剩下 n/2^k个元素。当k=log₂n 时候，只剩下一个元素，最多再比1次。因此，二分查找法最糟情况下需要比较 log₂n + 1 次。

下面来看java实现:

/**
 * 二分查找基础版
 * @param nums    待查找的升序数组
 * @param target    待查找的目标元素
 * @return    1.找到则返回索引; 2.找不到返回 -1
 */
public int binarySearchBasic(int[] nums, int target) {
    int low = 0, high = nums.length - 1;
    while (low <= high) {
        //int mid = (low + high) / 2;
        //int mid = low + ((high - low) >> 1);
        int mid = (low + high) >>> 1;

        if (target < nums[mid]) {
            high = mid - 1;
        } else if (nums[mid] < target) {
            low = mid + 1;
        } else {
            return mid;
        }
    }
    return -1;
}

这个代码需要解释一下，low、high、mid 都是指数组下标，其中 low 和 high 表示当前查找的区间范围，初始 low=0， high=nums.length - 1。mid 表示 [low, high] 的中间位置。我们通过对比 nums[mid] 与 target 的大小，来更新接下来要查找的区间范围，直到找到或者区间缩小为 0，就退出。

现在，着重强调一下容易出错的 3 个地方。

1.循环退出条件

注意是 low<=high，而不是 low<high。原因就是 low, high 作为边界条件，对应数组元素都是要查找的目标。

2.mid 的取值

mid就是区间 [low, high] 中间计算向下取整的值。实际上，mid = (low + high) / 2 这种写法是有问题的。因为如果 low 和 high 比较大的话，两者之和就有可能会溢出。改进的方法是将 mid 的计算方式写成 low+(high-low)/2。更进一步，如果要将性能优化到极致的话，我们可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1)。因为相比除法运算来说，计算机处理位运算要快得多。

当然 (low + high) >>> 1通过将数据无符号右移也是可以的。比如一个计算得到的整数超过了 int定义的范围,通过无符号右移1位,最高位就会补零,变成了正数且二进制转十进制的数也变成了原来的一半。

下面说下 >>> 1操作:

// 模拟循环体计算
int low = 0;
int high = Integer.MAX_VALUE - 1;
int m = low + ((high - low) >> 1);
low = m + 1;
m = low + ((high - low) >> 1);
System.out.println(m);  //1610612735

System.out.println(low);  //1073741824
System.out.println(high);  //2147483646
System.out.println(low + high);  //-1073741826
System.out.println(Integer.toBinaryString(low + high));  //10111111111111111111111111111110

//无符号右移1位操作如下:
//-1073741826 ->          10111111111111111111111111111110
//无符号右移1位,最高位补0
//1610612735 ->           01011111111111111111111111111111

int res = (low + high) >>> 1;
System.out.println(res);
// res = 1610612735

// res = m, 说明 >>> 1 也是同样的结果

3.low 和 high 的更新

low=mid+1，high=mid-1。注意这里的 +1 和 -1，如果直接写成 low=mid 或者 high=mid，就可能会发生死循环。

借助下图我们可以理解的更加直观:

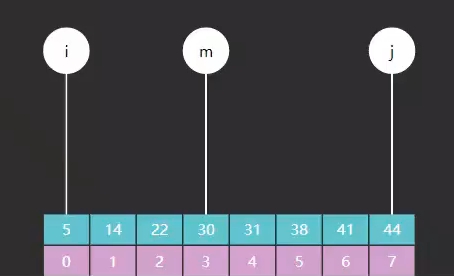
这个图里下标含义: i = low, j = high, m = mid 。

当我们初始值 low = 0, high = nums.length - 1 时,代表的是 low, high 所对应的下标元素都是要查找的目标, 此时循环条件就是 low <= high 。

当 target < nums[mid] 时, high = mid - 1 , 这里说明 下标mid所在的元素不是要找的元素且target元素在左边,则对应的高位 high 需要 -1。反之 low = mid + 1。

3.二分查找的改进版

/**
 * 二分查找改进版
 *
 * @param nums   待查找的升序数组
 * @param target 待查找的目标元素
 * @return : 1.找到则返回索引; 2.找不到返回 -1
 */
public int binarySearchAmeliorate(int[] nums, int target) {
    int low = 0, high = nums.length;
    while (low < high) {
        int mid = (low + high) >>> 1;
        if (target < nums[mid]) {
            high = mid;
        } else if (nums[mid] < target) {
            low = mid + 1;
        } else {
            return mid;
        }
    }
    return -1;
}

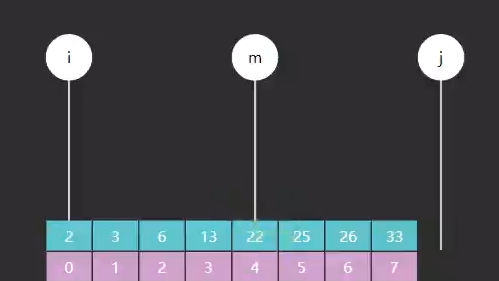
根据下图, 同样 i = low, j = high, m = mid 。

此时, high 在初始化时, high = nums.length。说明 high 只是作为一个查询边界，所指向的元素一定不是查找的目标,此时循环条件就是 low < high 。

当 target < nums[mid] 时, high = mid。此时的 nums[high]所对应的元素就不是目标值。

4.二分查找平衡

在基础版java实现中,若 target元素在mid下标的左边,则只要判断一个if语句，比较次数假设为 L；若 target元素在mid下标的右边,则要判断两个if语句,则比较次数就是 2 * L。

下面使用平衡版的实现:

/**
 * 二分查找平衡版
 *
 * @param nums   待查找的升序数组
 * @param target 待查找的目标元素
 * @return : 1.找到则返回索引; 2.找不到返回 -1
 */
public int binarySearchBalance(int[] nums, int target) {
    int low = 0, high = nums.length;
    while (low + 1 < high) {
        int mid = (low + high) >>> 1;
        // 循环内比较次数减少了
        if (target < nums[mid]) {
            high = mid;
        } else {
            low = mid;
        }
    }
    if (target == nums[low]) {
        return low;
    }
    return -1;
}

实现思想：

1. 左闭右开的区间，low指向的可能是目标，而 high指向的不是目标
2. 不奢望循环内通过mid 找出目标, 缩小区间直至剩 1 个, 剩下的这个可能就是要找的（通过low）
   • low + 1 < high 的含义是，在范围内待比较的元素个数 > 1
3. 改变low 边界时，它指向的可能是目标，因此不能 low + 1
4. 循环内的平均比较次数减少了
5. 时间复杂度 O(logn)

5.二分查找的变形问题

二分查找的代码模板必须牢记于心,这样针对下面的二分查找的变形问题是有帮助的。

你可以先写出二分查找模板套用,之后针对某个特殊条件进行微调。

二分查找代码模板:

public int binarySearch(int[] nums, int target) {
    int low = 0, high = nums.length - 1;
    while (low <= high) {
        //int mid = (low + high) / 2;
        //int mid = low + ((high - low) >> 1);
        int mid = (low + high) >>> 1;
        if (target < nums[mid]) {
            high = mid - 1;
        } else if (nums[mid] < target) {
            low = mid + 1;
        } else {
            return mid;
        }
    }
    return -1;
}

5.1 查找第一个值等于给定值的元素

上面的二分查找是最简单的一种，即有序数据集合中不存在重复的数据，我们在其中查找值等于某个给定值的数据。

如果我们将这个问题稍微修改下，有序数据集合中存在重复的数据，我们希望找到第一个值等于给定值的数据，这样之前的二分查找代码还能继续工作吗？

比如下面这样一个有序数组，其中，a[2]，a[3]，a[4] 的值都等于 6，是重复的数据。我们希望查找第一个等于 6 的数据，也就是下标是 2 的元素。

int [] nums = {1, 4, 6, 6, 6, 12, 15, 20, 22, 32, 49};

首先，我们先写出二分查找代码模板,这样就能确定某个 target = 6的位置。

题目是想在重复数据中要第一个下标，这样我们就可以在最后的 else 语句里判断该mid的元素左侧是不是 6。若是则继续缩小范围,否则返回该mid。

public int binarySearchLeftMost(int[] nums, int target) {
    int low = 0;
    int high = nums.length - 1;
    while (low <= high) {
        int mid = low + ((high - low) >> 1);
        if (nums[mid] > target) {
            high = mid - 1;
        } else if (nums[mid] < target) {
            low = mid + 1;
        } else {
            if ((mid == 0) || (nums[mid - 1] != target)) {
                return mid;
            } else {
                high = mid - 1;
            }
        }
    }
    return -1;
}

解释一下这段代码。nums[mid] 跟要查找的 target 的大小关系有三种情况：大于、小于、等于。对于 nums[mid]> target 的情况，我们需要更新 high= mid-1；对于 nums[mid]<target 的情况，我们需要更新 low=mid+1。这两点都很好理解。那当 nums[mid]=target 的时候应该如何处理呢？

如果我们查找的是任意一个值等于给定值的元素，当 nums[mid] 等于要查找的值时，nums[mid] 就是我们要找的元素。但是，如果我们求解的是第一个值等于给定值的元素，当 nums[mid] 等于要查找的值时，我们就需要确认一下这个 nums[mid] 是不是第一个值等于给定值的元素。

如果 mid 等于 0，那这个元素已经是数组的第一个元素，那它肯定是我们要找的；如果 mid 不等于 0，但 nums[mid] 的前一个元素 nums[mid-1] 不等于 target，那也说明 nums[mid] 就是我们要找的第一个值等于给定值的元素。

如果经过检查之后发现 nums[mid] 前面的一个元素 nums[mid-1] 也等于 target，那说明此时的 nums[mid] 肯定不是我们要查找的第一个值等于给定值的元素。那我们就更新 high = mid - 1，因为要找的元素肯定出现在 [low, mid-1] 之间。

当然，上面判断还是比较复杂。下面就是定义了一个变量,用来存储与target值相同的下标，之后我们继续缩小左侧的查询范围,这样最后找到的mid就是第一个下标。

public int binarySearchLeftMost(int[] nums, int target) {
    int low = 0, high = nums.length - 1;
    int idx = -1;
    while (low <= high) {
        int mid = (low + high) >>> 1;
        if (target < nums[mid]) {
            high = mid - 1;
        } else if (nums[mid] < target) {
            low = mid + 1;
        } else {
            // 记录 target相等的候选位置
            idx = mid;
            // 因为是找最左边的元素,则应该缩小右边界
            high = mid - 1;
        }
    }
    return idx;
}

5.2 查找最后一个值等于给定值的元素

前面的问题是查找第一个值等于给定值的元素，我现在把问题稍微改一下，查找最后一个值等于给定值的元素，又该如何做呢？

如果你掌握了前面的写法，那这个问题你应该很轻松就能解决。

public int binarySearchRightMost(int[] nums, int target) {
    int low = 0;
    int high = nums.length - 1;
    while (low <= high) {
        int mid = low + ((high - low) >> 1);
        if (nums[mid] > target) {
            high = mid - 1;
        } else if (nums[mid] < target) {
            low = mid + 1;
        } else {
            if ((mid == nums.length - 1) || (nums[mid + 1] != target)) {
                return mid;
            } else {
                low = mid + 1;
            }
        }
    }
    return -1;
}

如果 a[mid] 这个元素已经是数组中的最后一个元素了，那它肯定是我们要找的；如果 a[mid] 的后一个元素 a[mid+1] 不等于 value，那也说明 a[mid] 就是我们要找的最后一个值等于给定值的元素。

如果我们经过检查之后，发现 a[mid] 后面的一个元素 a[mid+1] 也等于 value，那说明当前的这个 a[mid] 并不是最后一个值等于给定值的元素。我们就更新 low=mid+1，因为要找的元素肯定出现在 [mid+1, high] 之间。

第二种写法:

public int binarySearchRightMost(int[] nums, int target) {
    int low = 0, high = nums.length - 1;
    int idx = -1;
    while (low <= high) {
        int mid = (low + high) >>> 1;
        if (target < nums[mid]) {
            high = mid - 1;
        } else if (nums[mid] < target) {
            low = mid + 1;
        } else {
            // 记录 target相等的候选位置
            idx = mid;
            low = mid + 1;
        }
    }
    return idx;
}

5.3 查找第一个大于等于给定值的元素

现在我们再来看另外一类变形问题。在有序数组中，查找第一个大于等于给定值的元素。

比如，数组中存储的这样一个序列：3, 4, 6, 7, 10。如果查找第一个大于等于 5 的元素，那就是 6。

实际上，实现的思路跟前面的那两种变形问题的实现思路类似，代码写起来甚至更简洁。

public int binarySearchFirstGreater(int[] nums, int target) {
    int low = 0, high = nums.length - 1;
    while (low <= high) {
        int mid = (low + high) >>> 1;
        if (target <= nums[mid]) {
            if (mid == 0 || nums[mid - 1] < target) {
                return mid;
            } else {
                high = mid - 1;
            }
        } else {
            low = mid + 1;
        }
    }
    return -1;
}

如果 nums[mid] 小于要查找的值 target，那要查找的值肯定在 [mid+1, high] 之间，所以，我们更新 low=mid+1。

对于 nums[mid] 大于等于给定值 target 的情况，我们要先看下这个 nums[mid] 是不是我们要找的第一个值大于等于给定值的元素。如果 nums[mid] 前面已经没有元素，或者前面一个元素小于要查找的值 target，那 nums[mid] 就是我们要找的元素。

如果 nums[mid-1] 也大于等于要查找的值 target，那说明要查找的元素在 [low, mid-1] 之间，所以，我们将 high 更新为 mid-1。

5.4 查找最后一个小于等于给定值的元素

现在，我们来看最后一种二分查找的变形问题，查找最后一个小于等于给定值的元素。

比如，数组中存储了这样一组数据：3, 5, 6, 8, 9, 10。最后一个小于等于 7 的元素就是 6。是不是有点类似上面那一种？实际上，实现思路也是一样的。

public int binarySearchLastLess(int[] nums, int target) {
    int low = 0;
    int n = nums.length;
    int high = n - 1;
    while (low <= high) {
        int mid = low + ((high - low) >> 1);
        if (nums[mid] > target) {
            high = mid - 1;
        } else {
            if ((mid == n - 1) || (nums[mid + 1] > target)) {
                return mid;
            } else {
                low = mid + 1;
            }
        }
    }
    return -1;
}

6.二分查找返回值应用

上面的二分查找变种介绍了如何查找第一个大于等于目标的方法。这里我们由变量值再简化一下新的写法，直接返回 low。

查找>=target 的最靠在索引:

/**
 * 二分查找 Leftmost
 *
 * @param nums   待查找的升序数组
 * @param target 待查找的目标元素
 * @return : >=target 的最靠在索引
 */
public int binarySearchLeftMost(int[] nums, int target) {
    int low = 0, high = nums.length - 1;
    int idx = -1;
    while (low <= high) {
        int mid = (low + high) >>> 1;
        /*if (target < nums[mid]) {
            high = mid - 1;
        } else if (nums[mid] < target) {
            low = mid + 1;
        } else {
            // 记录 target相等的候选位置
            idx = mid;
            // 因为是找最左边的元素,则应该缩小右边界
            high = mid - 1;
        }*/

        //简化:
        // 1.返回 low
        // 2.根据执行语句 high = mid - 1; 相同,将判断语句合并
        if (target <= nums[mid]) {
            // 目标只要小于中间值,都要向左侧收缩
            high = mid - 1;
        } else {
            // 目标只要大于中间值,都要向右侧收缩
            low = mid + 1;
        }
    }
    return low;
}

查找<=target 的最靠右索引：

/**
 * 二分查找 Rightmost
 *
 * @param nums   待查找的升序数组
 * @param target 待查找的目标元素
 * @return : <=target 的最靠右索引
 */
public int binarySearchRightMost(int[] nums, int target) {
    int low = 0, high = nums.length - 1;
    while (low <= high) {
        int mid = (low + high) >>> 1;
        if (target < nums[mid]) {
            high = mid - 1;
        } else {
            low = mid + 1;
        }
    }
    return low - 1;
}

几个名词

范围查询：

• 查询 x < 4，0 .. leftmost(4) - 1
• 查询 x <= 4，0 .. rightmost(4)
• 查询 4 < x，rightmost(4) + 1 .. \infty
• 查询 4 <= x， leftmost(4) .. \infty
• 查询 4 <= x <= 7，leftmost(4) .. rightmost(7)
• 查询 4 < x < 7，rightmost(4)+1 .. leftmost(7)-1

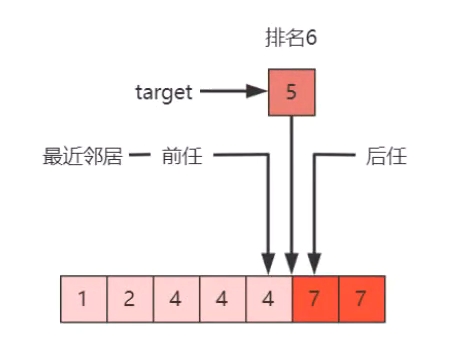
求排名：leftmost(target) + 1

• target 可以不存在，如：leftmost(5)+1 = 6
• target 也可以存在，如：leftmost(4)+1 = 3

求前任（predecessor）：leftmost(target) - 1

• leftmost(3) - 1 = 1，前任 a_1 = 2
• leftmost(4) - 1 = 1，前任 a_1 = 2

求后任（successor）：rightmost(target)+1

• rightmost(5) + 1 = 5，后任 a_5 = 7
• rightmost(4) + 1 = 5，后任 a_5 = 7

求最近邻居：

• 前任和后任距离更近者

7.练习

7.1 Leetcode 704 二分查找

704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1    

7.2 Leetcode 35 搜索插入位置

35.搜索插入位置

给定一个排序数组和一个目标值

• 在数组中找到目标值，并返回其索引
• 如果目标值不存在于数组中，返回它将会被按顺序插入的位置

例如

输入: nums = [1,3,5,6], target = 5
输出: 2

输入: nums = [1,3,5,6], target = 2
输出: 1

输入: nums = [1,3,5,6], target = 7
输出: 4

7.3 Leetcode 34 搜索开始结束位置

34. 在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题

示例 1：
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：
输入：nums = [], target = 0
输出：[-1,-1]

8.小结